Estimating the TAR Model
This example follows the empirical example found in Hansen (1996) and estimates a threshold model for quarterly GNP growth rates. The data file
gnp.dat contains seasonable adjusted GNP for 1947 to 1990 and is transformed to annualized quarterly growth rates:
//Load TSMT library
library tsmt;
//Real GNP data
//Seasonally adjusted and transformed in annualized quarterly growth rates
//1947-1990
//Load 'real_gnp' variable and perform 'ln' transformation
ln_gnp = loadd(__FILE_DIR $+ "gnp_4790.csv", "ln(real_gnp)");
y = (ln_gnp[2:rows(ln_gnp)] - ln_gnp[1:rows(ln_gnp)-1])*400;
Next all parameter values for the TAR estimation must be set
//Declare the structure
struct TARControl TAR0;
//Initialize the structure
TAR0 = TARControlCreate();
//Maximum number of lags considered
TAR0.p = 5;
//Lags to omit from the test
TAR0.omit = { 3, 4 };
//Trimming from top (r1) and bottom (r2) of data
TAR0.lowerQuantile = .15;
TAR0.upperQuantile = .85;
//Number of replications for Monte Carlo
TAR0.rep = 5000;
//Output and graph reporting
TAR0.printOutput = 1;
TAR0.graph = 1;
//Data start date and frequency
TAR0.dstart = 1947;
TAR0.freq = 4;
Finally, call the
GAUSS procedure
TARTest.
//Declare output structure
struct TAROut TARoutput;
//Estimate model
TARoutput = TARTest(y,TAR0);
This produces three graphs:
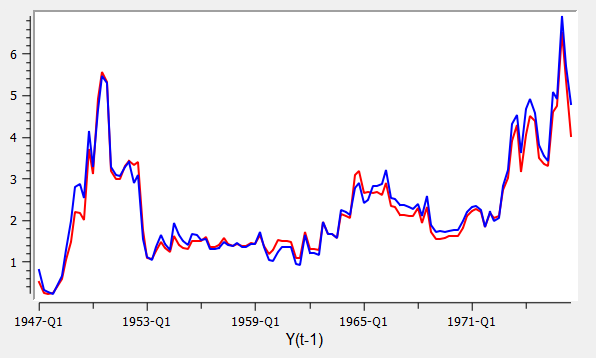
Plot for first lag

Plot for second lag

Plot for fifth lag
and prints the following output to the command/program window:
OLS Estimation of Null Linear Model
Variable Estimate S.E.
C 1.99225488 0.59341810
Y(t-1) 0.31753696 0.08929921
Y(t-2) 0.13197878 0.08801236
Y(t-5) -0.08696297 0.06763670
Residual Variance 15.960496
Searching over Threshold Variable: 1
Searching over Threshold Variable: 2
Searching over Threshold Variable: 3
Global Estimates
Threshold Variable Lag 2.0000000
Threshold Estimate 0.012572093
Error Variance 14.548361
Regime 1: Y(t-2) < 0.012572
Variable Estimate S.E.
C -3.21255539 2.12039565
Y(t-1) 0.51278104 0.24699822
Y(t-2) -0.92692272 0.30831951
Y(t-5) 0.38445656 0.24603002
Regime 1 Error Variance 23.533054
Regime 2: Y(t-2) > 0.012572
Variable Estimate S.E.
C 2.14186153 0.77389336
Y(t-1) 0.30085440 0.10132777
Y(t-2) 0.18484356 0.10131018
Y(t-5) -0.15813482 0.07335517
Regime 2 Error Variance 12.143010
Test Statistics and Estimated Asymptotic P-Values
Robust LM Statistics
SupLM 14.06847762 0.16940000
ExpLM 3.96481133 0.16620000
AveLM 4.68986250 0.27380000
Standard LM Statistics
SupLMs 18.24477743 0.94380000
ExpLMs 4.77627149 0.94320000
AveLMs 4.57209118 0.87960000



