GAUSS Bayesian Estimation Tools
The GAUSS Bayesian Estimation Tools package provides a suite of tools for estimation and analysis of a number of pre-packaged models. The internal GAUSS Bayesian models provide quickly accessible, full-stage modeling including data generation, estimation, and post-estimation analysis. Modeling flexibility is provided through control structures for setting modeling parameters, such as burn-in periods, total iterations and others.
GAUSS Bayesian internal models include
- Univariate and multivariate linear models
- Linear models with auto-correlated error terms
- HB Interaction and HB mixture models
- Probit models
- Logit models
- Dynamic two-factor model
- SVAR models with sign restrictions
Data loading and data generation
Users may load data into GAUSS for estimation and analysis using standard intrinsic GAUSS procedures. However, in addition, the Bayesian Analysis Module includes a data generation feature that allows users to specify true data parameters to build hypothetical data sets for analysis.
Individual modeling
Users can meet individual modeling needs by specifying key controls for the estimation algorithm including:
- Number of saved iterations
- Number of iterations to skip
- Number of burn-in iterations
- Total number of iterations
- Inclusion of an intercept
Easy to interpret stored results
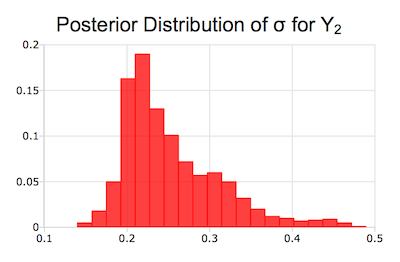
The Bayesian application module stores all results in a single output structure. In addition the Bayesian module graphs draws of all parameters and the posterior distributions for all parameters.
- Draws for all parameters at each iteration
- Posterior mean for all parameters
- Posterior standard deviation for all parameters
- Predicted values
- Residuals
- Correlation matrix between Y and Yhat
- PDF values and corresponding PDF grid for all posterior distributions
- Log-likelihood value (when applicable)
Sample output report for probit model
Model Type: Probit regression model
*************************************************************
Possible underlying (unobserved) choice generation:
Agent selects one alternative:
Y[ij] = X[j]*beta_i + epsilon[ij]
epsilon[ij]~N(0,Sigma)
*************************************************************
Y[ij] is mvar vector
Y[ij] is utility from subject i, choice set j, alternative k
where i = 1, ..., numSubjects
j = 1, ..., numChoices
k = 1, ..., numAlternatives - 1
*************************************************************
X[j] is numAlternative x rankX for choice j
*************************************************************
Pick alternative k if:
Y[ijk] > max( Y[ijl] )
for all k < mvar+1 and l not equal to k
Select base alternative if max(Y)<0
*************************************************************
Observed model:
*************************************************************
Choice vector C[ij] is a numAlternative vector of 0/1
beta_i = Theta'Z[i] + delta[i]
delta[i]~N(0,Lambda)
*************************************************************
Summary stats of independent data
*****************************************
Summary stats for X variables
*****************************************
Variable Mean STD MIN MAX
X1 0.33333 0.47538 0 1
X2 0.33333 0.47538 0 1
X3 0.33333 0.47538 0 1
X4 0.28648 0.20641 -0.083584 0.71157
X5 0.083333 0.59065 -1 1
*****************************************
Summary stats for Z variables
*****************************************
Variable Mean STD MIN MAX
Y1 -0.10328 1.1582 -6.1714 3.7266
Y2 -0.23821 1.1428 -6.1295 3.2853
Y3 -0.28473 1.2776 -5.4752 4.58
*****************************************
Summary stats for dependent variables
*****************************************
Variable Mean STD MIN MAX
Y1 -0.10328 1.1582 -6.1714 3.7266
Y2 -0.23821 1.1428 -6.1295 3.2853
Y3 -0.28473 1.2776 -5.4752 4.58
***********************************
MCMC Analysis Setup
***********************************
Total number of iterations: 1100.0
Total number of saved iterations: 1000.0
Number of iterations in transition period: 100.00
Number of iterations between saved iterations: 0.0000
Number of obs: 60.000
Number of independent variables: 5.0000
(excluding deterministic terms)
Number of dependent variables: 3.0000
********************************
MCMC Analysis Results
********************************
***********************************
Error Standard Deviation
***********************************
Variance-Covariance Means(Sigma)
Equation Y1 Y2 Y3
Y1 0.20831 0.078641 -0.12772
Y2 0.078641 0.26217 -0.078051
Y3 -0.12772 -0.078051 1
***********************************
Error Standard Deviation
***********************************
Variance-Covariance Means (Lambda)
Equation Beta1 Beta2 Beta3 Beta4 Beta5
Beta1 0.038024 0.0084823 0.0050414 -0.010463 -0.0044786
Beta2 0.0084823 0.038058 0.0061952 -0.0098521 0.0017846
Beta3 0.0050414 0.0061952 0.080755 -0.0086755 0.016158
Beta4 -0.010463 -0.0098521 -0.0086755 0.10271 -0.010493
Beta5 -0.0044786 0.0017846 0.016158 -0.010493 0.046216
***********************************
Theta for Z Equation 1.0000
***********************************
Variable PostMean PostSTD
Theta1 0.53176 0.43012
Theta2 0.43195 0.35411
Theta3 -0.011848 0.00015526
Theta4 -2.0511 -1.9772
Theta5 1.0605 1.1038
***********************************
Theta for Z Equation 2.0000
***********************************
Variable PostMean PostSTD
Theta1 0.90016 0.79037
Theta2 0.37388 0.19278
Theta3 -0.32424 -0.37066
Theta4 0.69154 0.85307
Theta5 -0.26623 -0.19126
***********************************
Theta for Z Equation 3.0000
***********************************
Variable PostMean PostSTD
Theta1 -0.24998 -0.2454
Theta2 -0.22883 -0.19728
Theta3 -0.043585 0.026509
Theta4 -0.29718 -0.30046
Theta5 0.52032 0.50741
Platform: Windows, Mac, and Linux
Requirements: GAUSS/GAUSS Engine/GAUSS Light v13.1 or higher